迷宫生成算法 | 张拓的博客

迷宫生成算法是创建迷宫的自动化方法。

基于图论的方法

基于图论的方法动画（随机深度优先搜索）
迷宫可以通过从预定的细胞排列（最常见的是矩形网格，但也可以使用其他排列）开始生成，它们之间有壁位置。这种预定的排列可以被视为一个连接的图，边缘代表可能的壁站点，节点代表细胞。然后，迷宫生成算法的目的可以被认为是制作一个子图，其中很难找到两个特定节点之间的路线。

如果子图未连接，则图中的某些区域被浪费，因为它们对搜索空间没有贡献。如果图形包含循环，则所选节点之间可能有多个路径。因此，迷宫生成通常被视为生成随机生成树。循环可能会混淆朴素迷宫求解器，可以通过在算法过程中向结果添加随机边来引入。

动画显示了迷宫生成步骤不在矩形网格上的图形。首先，计算机创建一个随机平面图G 以蓝色显示，及其双F 以黄色显示。其次，计算机使用选定的算法，例如深度优先搜索，将路径着色为红色。在遍历过程中，每当红边越过蓝边时，蓝色边缘被移除。最后，当访问完 F 的所有顶点时，F 被擦除并删除了 G 的两个边，一个用于入口，一个用于出口。

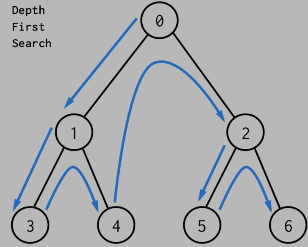
随机深度优先搜索

该算法也称为“递归回溯”算法，是深度优先搜索算法的随机版本。

这种方法经常通过堆栈实现，是使用计算机生成迷宫的最简单方法之一。考虑迷宫的空间是一个大的细胞网格（如一个大棋盘），每个细胞从四面墙开始。然后，计算机从随机单元格开始，选择一个尚未访问的随机相邻单元格。计算机移除两个单元之间的墙壁，并将新单元标记为已访问，并将其添加到堆栈中以方便回溯。计算机继续这个过程，一个没有未访问的邻居的单元被认为是死胡同。当处于死胡同时，它会通过路径回溯，直到到达具有未访问邻居的单元，通过访问这个新的、未访问的单元（创建一个新的交汇点）来继续路径生成。此过程一直持续到访问完每个单元格，导致计算机一直回溯到起始单元格。我们可以确保每个细胞都被访问过。

如上所述，此算法涉及深度递归，这可能会导致某些计算机体系结构上的堆栈溢出问题。通过将回溯信息存储在迷宫本身中，可以将算法重新排列成循环。这也提供了一种显示解决方案的快速方法，方法是从任何给定点开始并回溯到开头。

水平通道偏置
使用深度优先搜索生成的迷宫具有较低的分支因子，并且包含许多长走廊，因为该算法在回溯之前尽可能沿着每个分支进行探索。

递归实现

迷宫生成的深度优先搜索算法经常使用回溯来实现。这可以用以下递归例程来描述：

1.给定当前单元格作为参数
2.将当前单元格标记为已访问
3.当当前像元具有任何未访问的相邻像元时
- 1.选择一个未访问的邻居
- 2.移除当前单元格和所选单元格之间的墙
- 3.以递归方式调用所选单元格的例程

对于该区域中的任何初始单元格调用一次。

迭代实现

第一种方法的缺点是递归深度大 - 在最坏的情况下，例程可能需要在正在处理的区域的每个单元格上重复，这可能超过许多环境中的最大递归堆栈深度。作为一种解决方案，可以使用显式堆栈实现相同的回溯方法，该堆栈通常允许变得更大而不会造成伤害。

1.选择初始单元格，将其标记为已访问并将其推送到堆栈
2.当堆栈不为空时
- 1.从堆栈中弹出一个单元格并使其成为当前单元格
- 2.如果当前牢房有任何邻居没有被访问过
  - 1.将当前单元推送到堆栈
  - 2.选择一个未访问的邻居
  - 3.移除当前单元格和所选单元格之间的墙
  - 4.将所选单元格标记为已访问并将其推送到堆栈

随机克鲁斯卡尔算法

该算法是Kruskal算法的随机版本。

1.创建所有墙的列表，并为每个单元格创建一个集，每个单元格仅包含一个单元格。
2.对于每面墙，按某种随机顺序：
- 1.如果被这面墙分割的单元格属于不同的集合：
  - 1.移除当前墙。
  - 2.联接以前分割的单元格集。

有几种数据结构可用于对单元格集进行建模。使用脱节集数据结构的高效实现可以在几乎恒定的摊销时间内执行每个并集并查找两个集合的操作（特别是 $O(\alpha(V))$ 时间; $\alpha (x)<5$ 对于任何合理的值 $x$ )，因此该算法的运行时间基本上与迷宫可用的墙壁数量成正比。

无论墙列表最初是随机的还是从非随机列表中选择墙，这两种方式都同样容易编码，这无关紧要。

由于该算法的效果是从具有相同权重边缘的图形生成最小生成树，因此它倾向于产生相当容易解决的规则模式。

随机普里姆算法

该算法是Prim 算法的随机版本。

1.从满是墙壁的网格开始。
2.选择一个单元格，将其标记为迷宫的一部分。将单元格的墙壁添加到墙壁列表中。
3.虽然列表中有墙：
- 1.从列表中选择随机一堵墙。如果只访问壁分裂的一个细胞，则：
  - 1.将墙壁作为通道，并将未访问的牢房标记为迷宫的一部分。
  - 2.将单元格的相邻墙壁添加到墙壁列表中。
- 2.从列表中删除墙壁。

请注意，简单地在具有随机边权重的图上运行经典 Prim’s 将创建与 Kruskal 的迷宫在风格上相同的迷宫，因为它们都是最小的生成树算法。相反，此算法引入了样式变化，因为靠近起点的边缘具有较低的有效权重。

修改版本

尽管经典的 Prim 算法保留了边缘列表，但对于迷宫生成，我们可以维护相邻单元格的列表。如果随机选择的像元具有将其连接到现有迷宫的多条边，请随机选择其中一条边。这往往比上面基于边缘的版本分支略多。

简体版

通过随机选择与已访问过的单元格相邻的单元格，而不是跟踪所有单元格或边缘的权重，可以进一步简化该算法。

通常相对容易找到通往起始单元格的路，但在其他任何地方很难找到路。

威尔逊算法

主条目：循环擦除随机游走

上述所有算法都有各种各样的偏差：深度优先搜索偏向于长走廊，而Kruskal/Prim的算法偏向于许多短死胡同。另一方面，威尔逊的算法使用循环擦除的随机游走，从所有迷宫的均匀分布中生成一个无偏样本。

我们首先使用任意选择的一个单元格初始化迷宫。然后我们从任意选择的新单元格开始，并执行随机游走，直到我们到达已经在迷宫中的细胞——但是，如果在任何时候随机游走到达它自己的路径，形成一个循环，我们会在继续之前从路径中删除循环。当路径到达迷宫时，我们将其添加到迷宫中。然后，我们从另一个任意起始单元格执行另一个循环擦除随机漫游，重复直到所有单元格都被填充。

无论我们使用哪种方法任意选择起始细胞，此过程都保持公正。因此，为了简单起见，我们始终可以按从左到右、从上到下的顺序选择第一个未填充的单元格。

Aldous-Broder算法

Aldous-Broder 算法还生成均匀生成树。

1.随机选择一个单元格作为当前单元格，并将其标记为已访问。
2.虽然有未访问的单元格：
- 1.随机选择一个邻居。
- 2.如果所选邻居尚未被访问：
  - 1.移除当前像元和所选相邻单元之间的墙。
  - 2.将所选邻居标记为已访问。
- 3.使所选相邻要素成为当前像元。

递归除法

迷宫可以用递归除法创建，这种算法的工作方式如下：从没有墙壁的迷宫空间开始。称之为密室。用随机定位的墙壁（或多个墙壁）划分房间，其中每个墙壁都包含一个随机定位的通道开口。然后在子腔室上递归重复该过程，直到所有腔室的尺寸最小。这种方法导致迷宫的长直墙穿过其空间，更容易看到要避开的区域。

例如，在矩形迷宫中，在随机点上构建彼此垂直的两面墙。这两面墙将大房间分成四个较小的房间，由四面墙隔开。随机选择四面壁中的三面，并在三面壁中的每一面壁的随机点开一个细胞宽的洞。以这种递归方式继续，直到每个腔室在两个方向中的任何一个方向上都有一个单元格的宽度。

简单算法

存在其他算法，只需要足够的内存来存储 2D 迷宫的一行或 3D 迷宫的一个平面。Eller的算法通过存储当前行中的哪些单元通过前几行中的单元连接来防止循环，并且从不删除已经连接的任何两个单元格之间的墙壁。响尾蛇算法从沿整个顶行的开放通道开始，随后的行由较短的水平通道组成，其中一个与上面的通道相连。响尾蛇算法自下而上解决起来很简单，因为它没有向上的死胡同。给定起始宽度，两种算法都会创建无限高度的完美迷宫。

大多数迷宫生成算法都需要维护其中细胞之间的关系，以确保最终结果是可解决的。然而，有效的简单连接迷宫可以通过独立聚焦每个细胞来生成。二叉树迷宫是一个标准的正交迷宫，其中每个单元格总是有一个通向左或向左的通道，但从不两者兼而有之。要创建一个二叉树迷宫，每个单元格掷硬币以决定是添加一条通向还是向左的通道。始终为边界上的单元格选择相同的方向，最终结果将是一个有效的简单连接迷宫，看起来像二叉树，左上角是其根。与响尾蛇一样，二叉树迷宫在偏向方向上没有死胡同。

为每个单元格掷硬币的一种相关形式是使用正斜杠和反斜杠字符的随机混合来创建图像。这不会生成一个有效的简单连接的迷宫，而是一系列闭环和单曲通道。Commodore 64的手册提供了使用此算法的基本程序，使用PETSCII对角线图形字符代替，以获得更平滑的图形外观。

元胞自动机算法

某些类型的元胞自动机可用于生成迷宫。两个著名的元胞自动机，迷宫和迷宫，具有规则字符串B3 / S12345和B3 / S1234。在前者中，这意味着如果细胞至少有一个和最多五个邻居，它们就会从一代存活到下一代。在后者中，这意味着如果细胞有一到四个邻居，它们就会存活。如果一个细胞正好有三个邻居，它就诞生了。它类似于康威的生命游戏，因为在任何一代中没有与 1、4 或 5 个其他活细胞相邻的活细胞的模式的行为都与它相同。但是，对于大型模式，它的行为与 Life 非常不同。

对于随机起始模式，这些生成迷宫的元胞自动机将演变成复杂的迷宫，具有轮廓清晰的墙壁轮廓。与具有规则B3/S12345的迷宫相比，具有规则B3 / S1234的迷宫倾向于产生更长和更直的走廊。由于这些元胞自动机规则是确定性的，因此生成的每个迷宫都由其随机起始模式唯一确定。这是一个明显的缺点，因为迷宫往往是相对可预测的。

像上面描述的一些基于图论的方法一样，这些元胞自动机通常从单个起始模式生成迷宫;因此，找到通往起始单元格的路通常相对容易，但在其他任何地方更难找到路。

参考资料

本文翻译自
https://en.wikipedia.org/wiki/Maze_generation_algorithm#Randomized_depth-first_search